Divers Infinis

Mise en évidence géométrique des divers infinis.


Prenons un repère orthonormé et étudions les possibilités pour relier le point A (1,0) au point B (0,1) en n'effectuant que des déplacements horizontaux ou verticaux.

Le premier qui vient à l'esprit est de partir de A, de monter de 1 et d'aller à gauche de 1 pour rejoindre B, la distance parcourue sera donc égale à 2.

On peut également partir de A, monter de 1/2, aller à gauche de 1/2, remonter de 1/2 et aller de nouveau à gauche de 1/2 pour rejoindre B. On aura toujours parcouru une distance égale à 2.

On peut faire encore la même chose avec 1/4, ... pour obtenir ce que l'on observe sur l'image.



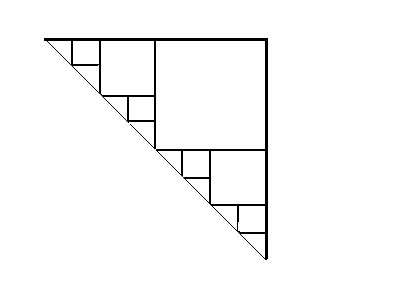
La distance parcourue est toujours égale à 2.

Mais seulement, voilà le problème. Si on effectue l'opération décrite précédemment avec des distances pour les montées et les revirements à gauche qui tendent vers 0 (cela revient à monter de 1/(2^n) vers le haut et sur la gauche avec n qui tend vers l'infini), on devrait toujours avoir une distance de 2 et on obtient petit à petit une droite.

Or, la distance de cette droite n'est pas égale à 2 mais à racine(2) en tant que diagonale d'un carré de côté 1.

En fait, la réponse est donnée par Cantor à la fin du XIXème siècle : cela vient d'une différence d'infinis. Les tournants successifs de plus en plus petits "tendent vers l'infini des nombres entiers alors que la droite est l'infini des nombres réels". Le second est beaucoup plus grand que le premier. Les tournants successifs se rapprochent de la droite mais ne peuvent jamais s'identifier à elle.

Le premier infini à été baptisé Aleph 0 et le second Aleph 1.


Source : L'équation du nénuphar - Albert Jacquard

 
 
~somonovitz~ Publié le : 12/03/2006

 

En cas de conflit avec cet article (problème de droits d'auteur, etc.) vous pouvez en demander la suppression auprès d'un administrateur du site.

Il faut être membre du site afin de pouvoir rajouter un complément d'information sur un article.